【例】甲、乙、丙同时给100盆花浇水,已知甲浇了78盆,乙浇了68盆,丙浇了58盆,那么3人都浇过的花最少有()盆?
A.4B.5
C.6 D.7
【答案及解析】A。法一:结合容斥原理比较抽象的一类构造问题。当题干问的是AnBnC的最小值时,该类型题做题套路较简单。分别把甲、乙、丙没浇过的花求出来:22、32、42,加起来共有96盆,用总数100-96即为答案。类似的题目都可以这样来操作。考试中碰到四集合的情况,方法相同。
法二:根据极端思维,要让3人都浇过的花尽可能少,则让三个人尽可能分散开浇,假设甲从第1盆浇,浇到78盆,丙从最后一盆浇,浇到倒数58盆,则两人有78+58-100=36盆共同浇过,剩余100-36=64盆两人单独浇过,现在乙浇了68盆,让乙先浇甲丙单独浇的64盆,则还剩4盆,乙必须浇在甲丙浇的花上,说明三人共浇的至少有4盆。可简单画个图来表示:
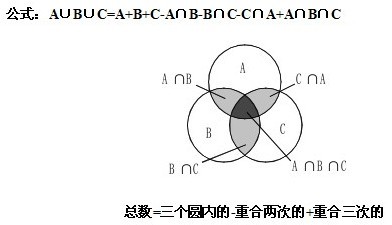
法三:该题也可以用公式:A+B+C-2×总数=78+68+58-2×100=4。
解释:假设每盆花被浇了2次,则共浇了200次。甲、乙、丙共浇了204次,则多出4次,说明有4盆花又被浇了一次,共浇了三次。说明被甲、乙、丙都浇过的有4次。
对于四集合则为:A+B+C+D-3×总数
 爱华网
爱华网