转载自 deepthink_2010
最终编辑 shuting_guo
1.使用模板处理图像相关概念:
模板:矩阵方块,其数学含义是一种卷积运算。
卷积运算:可看作是加权求和的过程,使用到的图像区域中的每个像素分别与卷积核(权矩阵)的每个元素对应相乘,所有乘积之和作为区域中心像素的新值。
卷积核:卷积时使用到的权,用一个矩阵表示,该矩阵与使用的图像区域大小相同,其行、列都是奇数,是一个权矩阵。
卷积示例:
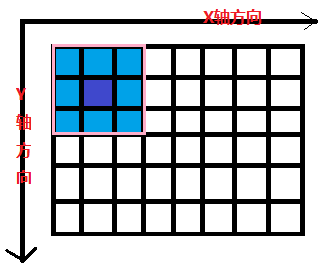
假设3 * 3的像素区域R与卷积核G分别为:
则卷积运算为:
R5(中心像素)=R1G1 + R2G2 + R3G3 + R4G4 + R5G5 + R6G6 + R7G7 + R8G8 + R9G9
2、使用模板处理图像时涉及到的问题:
边界问题:当处理图像边界像素时,卷积核与图像使用区域不能匹配,卷积核的中心与边界像素点对应,卷积运算将出现问题。
处理办法:
A.忽略边界像素,即处理后的图像将丢掉这些像素。
B.保留原边界像素,即copy边界像素到处理后的图像。
3、常用模板:
(a)低通滤波器
(b)高通滤波器
(c)平移和差分边缘检测
(d)匹配滤波边缘检测
(e)边缘检测
(f)梯度方向边缘检测
4、我们来看一下一维卷积的概念.
卷积(convolution,另一个通用名称是德文的Faltung)的名称由来,是在于当初定义它时,定义成integ(f1(v)*f2(t-v))dv,积分区间在0到t之间。举个简单的例子,大家可以看到,为什么叫“卷积”了。比方说在(0,100)间积分,用简单的辛普生积分公式,积分区间分成100等分,那么看到的是f1(0)和f2(100)相乘,f1(1)和f2(99)相乘,f1(2)和f2(98)相乘,.........等等等等,就象是在坐标轴上回卷一样。所以人们就叫它“回卷积分”,或者“卷积”了。
连续空间的卷积定义是f(x)与g(x)的卷积是f(t-x)g(x)在t从负无穷到正无穷的积分值.t-x要在f(x)定义域内,所以看上去很大的积分实际上还是在一定范围的.
实际的过程就是f(x)先做一个Y轴的反转,然后再沿X轴平移t就是f(t-x),然后再把g(x)拿来,两者乘积的值再积分.想象一下如果g(x)或者f(x)是个单位的阶越函数.那么就是f(t-x)与g(x)相交部分的面积.这就是卷积了.
卷积运算满足交换律,也就是说:f与g进行卷积完全等于g与f进行卷积。
由两个函数f和g进行卷积而得到的函数f*g,一般要比原来的f和g都要光滑。所以在图像处理中对图像进行卷积后会使原图像模糊。因为卷积具有平滑作用。
有趣的是,如果把两个人的照片互相进行卷积,所得到的照片,就同时和这两个人都很相像。
把积分符号换成求和就是离散空间的卷积定义了.
那么在图像中卷积是什么意思呢,就是图像就是图像f(x),模板是g(x),然后将模版g(x)在模版中移动,每到一个位置,就把f(x)与g(x)的定义域相交的元素进行乘积并且求和,得出新的图像一点,就是被卷积后的图像.模版又称为卷积核.卷积核做一个矩阵的形状。
5、卷积运算时的核函数
在Matlab中,对图像进行卷积运算时,都要先得到一个核函数,其实就是模板。其函数调用是:
>> G=fspecial('gaussian',5,0.5)
G =
0.00000.00000.00020.00000.0000
0.00000.01130.08370.01130.0000
0.00020.08370.61870.08370.0002
0.00000.01130.08370.01130.0000
0.00000.00000.00020.00000.0000
>> G=fspecial('gaussian',5,1.5)
G =
0.01440.02810.03510.02810.0144
0.02810.05470.06830.05470.0281
0.03510.06830.08530.06830.0351
0.02810.05470.06830.05470.0281
0.01440.02810.03510.02810.0144
能够看出来,fspesial()函数的第一个参数表示返回高斯核函数(低通滤波器、模板等名称其实都一样)。第二个参数“5”表示该模板的大小,是5X5的矩阵。第三个参数是sigma了。
 爱华网
爱华网