首先月亮的自转周期和它围绕地球公转的周期是一致的都是28天。
我想用圆柱体代表月球这个球体,咱们看到的月球正面是黄色的看不到的月球背面用白色表示。
完全不会看到月球背面的情形:
如果月球不自转,将会是如下情况(可以看到完整背面):
如果月球自转周期不是与公转周期相同的28天,则情况介于两者之间。
附:为何月球自转和公转周期一致,科学家的解释:
这个问题从力学分析上来讲比较费劲,可以从能量的角度来考虑。首先要明白两个问题,第一是从月球质量分布上来说,月球并不是一个绝对的球体,第二,地球的海洋对月球有一个潮汐作用(岩石,土地等也有潮汐力,但较海洋比较微弱)。
起初,月球的公转和自传并不是同步的,这样当月球围绕地球做公转时,潮汐力对月球就有一个作用,这个作用对月球来说有两个效应,第一就是公转和自传的倍率关系,就是说当月球相对地球来看(以地球为参照系)自传周期是公转周期的整数倍时,这时潮汐力对月球来说就是一个非常规律的变化作用,这时月球的自转就会稳定下来,而当自转与公转不是倍数关系时,潮汐力对月球的作用就显得无规律,而这个无规律的效果就是使月球的自转趋于公转的倍数,最终月球的自传会稳定在他公转周期的一个倍数上,至于是多少倍要看他本身的自转周期了,比若说自转是公转的3。5倍,那么当月球自转稳定下来时他肯定是3倍公转周期,如果是1。2倍最终就是与公转同步。
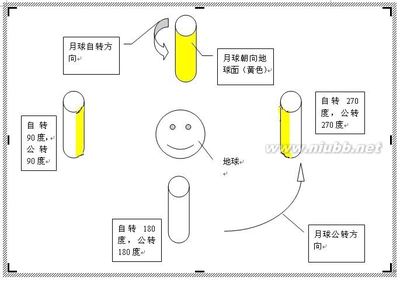
既然公转与自转的周期相同了,那么我们看到的月球自然只是同一个面了,所以看不到月球的背部。
刚才提到潮汐力对月球有两个效应,现在还有第二个效应没有说,那就是月球在远离地球,这也是潮汐力使然。那么我们知道考虑地月系统来说,月球原理地球肯定是机械能变大了(虽然动能小了,但是引力势能增加的更大),那么月球是如何获得这些能量而远离地球呢?那么这里就牵扯到了潮汐力对地球的作用了,刚才只考虑潮汐对月球的两个效应,那么对于地月系统来说地球并没有动能,引力势能刚才已经考虑了,那么还有什么能量的参与呢?那就是地球的自转动能(转动动能),月球原理地球而去的同时,我们地球的自转变慢了,也就是说在很久以前地球的一天要比现在短,而到很久的将来地球的一天要比现在长。这就是我们地月系统的现在正在进行的变化。
 爱华网
爱华网



