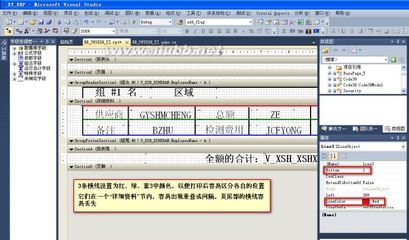
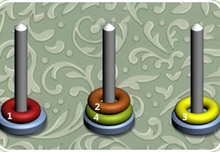
假设有不同大小的光碟标签ñ从1到n按照它们的大小的升序排列。在初始状态是随机的N光盘上三极堆积,现在你必须要了解最少的动作把初始状态的目标。
该举措的要求为以下几种:
1)你只能一次移动一个圆盘;
2)较大的光盘是不允许在一个较小的一栈
current和target分别表示开始状态的结束状态。
这个问题和Hanoi问题相似,可以这样做
1找到最大的需要移动的盘k
2将小于此盘的1...k-1摞成一堆
3腾出目标位置,移动k
4再次找到需要移动的k,重复3直到k=1
对于步骤2实现起来比较难,可以将2再次看成一个问题,用分治算法来做
make_tower(k,current)//将1...k落到k在的位置
if k=1then return
ifk=2
ifcurrent[k]≠current[k-1]
then将k移到k+1上
return
ifk,k-1,k-2分别位于不同位置
thenmake_tower(k-2,current)
将k-1移到k上
Hanoi(current,k-2,current[k-2],current[k-1],current[k])
return
make_tower(k-1,current)
ifk和k-1不在同一个位置
thentemp←除k和k-1的位置
Hanoi(current,k-1,current[k-1],temp,current[k])
这样问题迎刃而解了
代码
#include<stdio.h>
int count=0;
int pick_top(char c[],char a)
{
int i=1;
while(c[i]!=a)
i++;
return i;
}
void Hanoi(char current[],int k,char a,char b,char c)
{
int i;
if(k==1)
{
i=pick_top(current,a);
printf("%c-->%cn",a,c);
count++;
current[i]=c;
return;
}
Hanoi(current,k-1,a,c,b);
printf("%c-->%cn",current[k],c);
count++;
current[k]=c;
Hanoi(current,k-1,b,a,c);
}
void make_tower(char c[],int n)
{
char temp;
if(n==1)
return;
if(n==2)
{
if(c[1]!=c[2])
{
printf("%c-->%cn",c[1],c[2]);
count++;
c[1]=c[2];
}
return;
}
if(c[n]!=c[n-1]&&c[n]&&c[n-2]&&c[n-1]!=c[n-2]){//n,n-1,n-2都不在同一个盘子上
make_tower(c,n-2);
//将n-1移到n上
printf("%c-->%cn",c[n-1],c[n]);
count++;
temp=c[n-1];
c[n-1]=c[n];
Hanoi(c,n-2,c[n-2],temp,c[n]);
return;
}
make_tower(c,n-1);
if(c[n-1]!=c[n])
{
temp='A'+'B'+'C'-c[n]-c[n-1];
Hanoi(c,n-1,c[n-1],temp,c[n]);
}
}
int main()
{
char current[6]={0,'C','C','C','B','B'};
char target[6]={0,'C','A','B','B','B'};
int k=6;
char temp;
while(current[k]!=target[k]&&k>0)//找到第一个最大的不符合要求的盘子
k--;
if(k>2)//如果k>2,把1...k-1移到k-1上
make_tower(current,k-1);
while(k>1)
{
if(current[k]!=target[k])
{
if(current[k]==current[k-1])
{
temp='A'+'B'+'C'-current[k]-target[k];
Hanoi(current,k-1,current[k-1],target[k],temp);
}
elseif(current[k-1]==target[k])
{
temp='A'+'B'+'C'-current[k]-target[k];
Hanoi(current,k-1,current[k-1],current[k],temp);
}
printf("%c-->%cn",current[k],target[k]);
count++;
current[k]=target[k];
}
k--;
}
if(current[1]!=target[1])
{
printf("%c-->%cn",current[1],target[1]);
count++;
current[1]=target[1];
}
printf("%dn",count);
}
 爱华网
爱华网