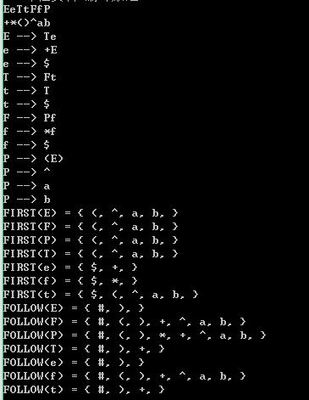
对于终结符和非终结符的理解:
终结符:通俗的说就是不能单独出现在推导式左边的符号,也就是说终结符不能再进行推导。
非终结符:不是终结符的都是非终结符。
如:A->B,则A是非终结符;A->id,则id是终结符。
(一般书上终结符用小写,非终结符用大写。)
文法产生语言句子的基本思想:
从识别符号(开始符)开始,把当前产生的符号串中的非终结符替换为相应规则右部的符号串,直到全部由终结符组成。所以文法产生句子的基本思想就是基于产生式(例如A->num)的替换,当所有的非终结符都被终结符替换时,推导结束。
FIRST集求法:
我对First集的理解:first集应该就是求一个表示文法的字串(一般指非终结符,终结符的first集就是它自身)开头的所有可能出现的字符的集合。例如A->aC|bB|cD,根据这个产生式,就可以知道,非终结符A,被替换后,它开头可能出现字符有a、b、c,所以{a,b,c}是First(A)的一个子集。
求First集的步骤:
若X->a..,则将终结符a加入FIRST(X)中;
若X->e,则将终结符e加入FIRST(X)中(e表示空集);
若X->BC..D,则将First(B)所有元素(除了空集)加入First(A),然后检测First(B),若First(B)中不存在空集,即e,则停止,若存在则向B的后面查看,将First(C)中所有元素(除了空集)加入First(A),然后再检测First(C)中是否有e...直到最后,若D之前的所有非终结符的First集中都含有e,则检测到D时,将First(D)也加入First(A),若First(D)中含有e,则将e加入First(A)。
对于第三条,其实也很好理解,就是说当X推导出一个字串时,D前面的非终结符都可能推出空串,这个时候,X推出的串的首部,就不是那些推出空串的非终结符了,而是这些推出空串的非终结符后面的文法符号所推导出的字串。
FOLLOW集的求法:
对Follow集,其实也差不多,它应该是指非终结符推出的字串最末端后可能出现的所有字符的集合。例如Follow(U)所表达的是句型中非终结符U所有可能的后随终结符号的集合,特别地,“$”是识别符号的后随符。注意Follow集合是从开始符号S开始推导。
求Follow集的步骤:
对文法开始符号S,置$于FOLLOW(S)中;
对于产生式:A->aBC,将除去空集e的First(C)加入Follow(B)中;
对于产生式:A->aB或者A->aBC,(其中C可以推导出空串,C=>*e),则将Follow(A)加入Follow(B)中。
(注意:此处a可以是空,也可以是其他文法符号);
对第二条步骤的理解:Follow(B)是B推出的串末端后的字符集合,在A->aBC的情形下,B推出串末端后的字符集,也就是C推出串首部字符的集合,即First(C)中除去e的集合。
对于第三条,其实也比较好理解,A->aB,那么A推出字串的末端后字符集合,与B推出字串的末端后字符集合,是等价的。
另一种理解:
FOLLOW集的求法:
对Follow集,其实也差不多,它应该是指非终结符推出的字串最末端后可能出现的所有字符的集合。例如Follow(U)所表达的是句型中非终结符U所有可能的后随终结符号的集合,特别地,“$”是识别符号的后随符。注意Follow集合是从开始符号S开始推导。
求Follow集的步骤:
对文法开始符号S,置$于FOLLOW(S)中;
对于产生式:A->aBC,将除去空集e的First(C)加入Follow(B)中;
对于产生式:A->aB或者A->aBC,(其中C可以推导出空串,C=>*e),则将Follow(A)加入Follow(B)中。
(注意:此处a可以是空,也可以是其他文法符号);
对第二条步骤的理解:Follow(B)是B推出的串末端后的字符集合,在A->aBC的情形下,B推出串末端后的字符集,也就是C推出串首部字符的集合,即First(C)中除去e的集合。
对于第三条,其实也比较好理解,A->aB,那么A推出字串的末端后字符集合,与B推出字串的末端后字符集合,是等价的。
First集合的求法:
First集合最终是对产生式右部的字符串而言的,但其关键是求出非终结符的First集合,由于终结符的First集合就是它自己,所以求出非终结符的First集合后,就可很直观地得到每个字符串的First集合。
1.直接收取:对形如U-a…的产生式(其中a是终结符),把a收入到First(U)中
2.反复传送:对形入U-P…的产生式(其中P是非终结符),应把First(P)中的全部内容传送到First(U)中。
Follow集合的求法:
Follow集合是针对非终结符而言的,Follow(U)所表达的是句型中非终结符U所有可能的后随终结符号的集合,特别地,“#”是识别符号的后随符。
1.直接收取:注意产生式右部的每一个形如“…Ua…”的组合,把a直接收入到Follow(U)中。
2.直接收取:对形如“…UP…”(P是非终结符)的组合,把First(P)除ε直接收入到Follow(U)中。
3.反复传送:对形如P-…U的产生式(其中U是非终结符),应把Follow(P)中的全部内容传送到Follow(U)中。(或P-…UB且First(B)包含ε,则把First(B)除ε直接收入到Follow(U)中,并把Follow(P)中的全部内容传送到Follow(U)中)
First集合求法就是:能由非终结符号推出的所有的开头符号或可能的ε,但要求这个开头符号是终结符号。如此题A可以推导出a和ε,所以FIRST(A)={a,ε};同理FIRST(B)={b,ε};S可以推导出aBc,还可以推导出bc,还可以推导出c,所以FIRST(S)={a,b,c}。
Follow集合的求法是:紧跟随其后面的终结符号或#。但文法的识别符号包含#,在求的时候还要考虑到ε。具体做法是把所有包含你要求的符号的产生式都找出来,再看哪个有用。Follow(S)={#} 如求A的,产生式:S→ABc A→a|ε ,但只有S→ABc有用。跟随在A后年的终结符号是FIRST(B)={b,ε},当FIRST(B)的元素为ε时,跟随在A后的符号就是c,所以Follow(A)={b,c} 同理Follow(B)={c}。
 爱华网
爱华网


