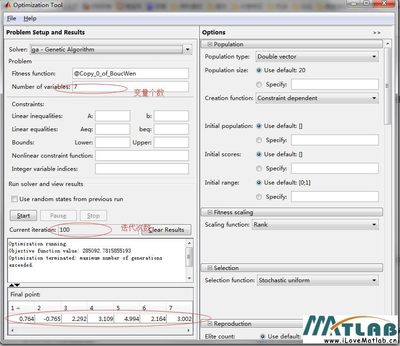
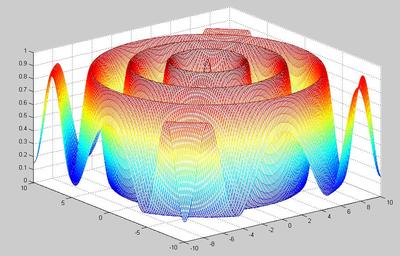
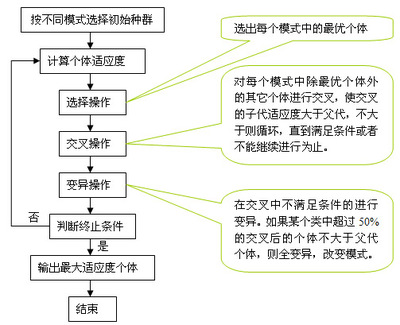
前一阵子搞了一些遗传算法的东西,使用的是gaot遗传算法工具箱,这个算法工具箱还是蛮使用的,不过貌似很久不更新了,将就用吧!
貌似网上下载的工具箱代码有错误,不妨检查一下,f2b函数需要如下修改
function [bval] = function(fval,bounds,bits)改为function [bval] =f2b(fval,bounds,bits)
工具箱中的Contents.m文件包含了各个文件的介绍,主要的两个函数是ga.m和initializega.m,前者是遗传算法的训练函数,后者是产生初始种群的函数。核心函数说明如下:
(1)function[pop]=initializega(num,bounds,eevalFN,eevalOps,options)--初始种群的生成函数
【输出参数】
pop--生成的初始种群
【输入参数】
num--种群中的个体数目
bounds--代表变量的上下界的矩阵
eevalFN--适应度函数
eevalOps--传递给适应度函数的参数
options--选择编码形式(浮点编码或是二进制编码)[precisionF_or_B],如
precision--变量进行二进制编码时指定的精度
F_or_B--为1时选择浮点编码,否则为二进制编码,由precision指定精度)
(2)function[x,endPop,bPop,traceInfo]=ga(bounds,evalFN,evalOps,startPop,opts,...
termFN,termOps,selectFN,selectOps,xOverFNs,xOverOps,mutFNs,mutOps)--遗传算法函数
【输出参数】
x--求得的最优解
endPop--最终得到的种群
bPop--最优种群的一个搜索轨迹
【输入参数】
bounds--代表变量上下界的矩阵
evalFN--适应度函数
evalOps--传递给适应度函数的参数
startPop-初始种群
opts[epsilonprob_opsdisplay]--opts(1:2)等同于initializega的options参数,第三个参数控制是否输出,一般为0。如[1e-610]
termFN--终止函数的名称,如['maxGenTerm']
termOps--传递个终止函数的参数,如[100]
selectFN--选择函数的名称,如['normGeomSelect']
selectOps--传递个选择函数的参数,如[0.08]
xOverFNs--交叉函数名称表,以空格分开,如['arithXoverheuristicXoversimpleXover']
xOverOps--传递给交叉函数的参数表,如[20;23;20]
mutFNs--变异函数表,如['boundaryMutationmultiNonUnifMutationnonUnifMutationunifMutation']
mutOps--传递给交叉函数的参数表,如[400;61003;41003;400]
网站http://www.caogenit.com/caogenxueyuan/yingyongfangxiang/rengongzhineng/1092.html里有代码的使用的例子。
此工具箱中自带了几个例子,很有参考价值
% Demonstrations
% gademo1.m Introductory demo ofGAOT
% gademo2.m Multi-dimensional demo of GAOT
% gademo3.m Reference for GAOT
% floatExample.m Example usingfloat representation
% floatGradExample.m Example exploring learning(Lamarckian andBaldwinian)
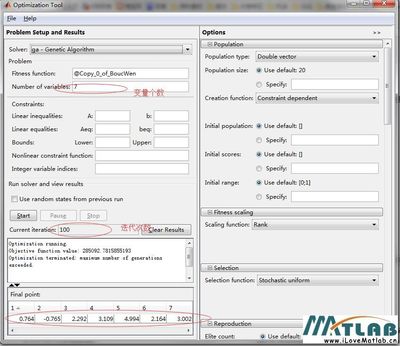
% binaryExample.m Example usingbinary representation
% orderBasedExample.m Example using order-basedrepresentation
gademo1脚本一步一步解释给你工具箱的使用过程
gademo2貌似是个多维的例子,意义不大
gademo3全是文字介绍,说明了工具箱的各个函数的意义
floatExample介绍了使用浮点型编码的一个使用实例
binaryExample介绍了一个使用二进制编码的实例,这两个实例基本把这个工具箱用法介绍齐了。不过这两个例子每步都会停下来,直接看代码就行了。
如下代码从gademo1中整理而来
% 遗传算法测试
clc
close all
clear all
bound = [0 9]; % 设置x的范围
% 原函数
figure
fplot('x + 10*sin(5*x)+7*cos(4*x)',bound) % 绘制函数图形
hold on
% 产生初始种群
initPop = initializega(10,bound,'gaDemo1Eval_GJ'); %10表示初始种群的个数,默认是浮点编码
plot(initPop(:,1),initPop(:,2),'g+') % 绘制初始种群
% 遗传一代的结果
[x endPop] = ga(bound,'gaDemo1Eval_GJ',[],initPop,[1e-6 11],'maxGenTerm',1,...
'normGeomSelect',[0.08],['arithXover'],[20],'nonUnifMutation',[2 1 3]); %gaDemo1Eval_GJ里需要按标准的格式编写,其他参数为设置遗传算法的参数
plot(endPop(:,1),endPop(:,2),'ro')
% 遗传25代的结果
[x endPop bpop trace] =ga(bound,'gaDemo1Eval_GJ',[],initPop,[1e-6 11],'maxGenTerm',25,...
'normGeomSelect',[0.08],['arithXover'],[2],'nonUnifMutation',[225 3]);
plot (endPop(:,1),endPop(:,2),'y*')
% 看遗传效果
figure
plot(trace(:,1),trace(:,3),'y-')
hold on
plot(trace(:,1),trace(:,2),'r-')
legend({'the best solution', 'the average of thepopulation'})
xlabel('Generation');
ylabel('Fittness');
其中的gaDemo1Eval_GJ函数代码如下
function [sol, val] = gaDemo1Eval_GJ(sol,options)
% f(x)=x+10sin(5x)+7cos(4x)
%
% val - the fittness of this individual
% sol - the individual, returned to allow for Lamarckianevolution
% options - [current_generation]
%
% Note that the evaluation function must take twoparameters,
% sol and options. Sol is a row vector ofn+1 elements where
% the first n elements are the parametersof interest. The
% n+1'th element is the value of thissolution. The options
% matrix is a row matrix of
% [current generation, eval options]
x = sol(1);
val = x + 10*sin(5*x)+7*cos(4*x);
end
运行结果如下,其中绿色点为初始种群,红色为一次遗传算法的结果,黄色点为25次遗传算法的结果,可以看到都已经收敛到了全局最大值点。
下面的图形表示了遗传算法的整个遗传过程
 爱华网
爱华网