回归分析是一种应用很广的数量分析方法,用于分析事物间的统计关系,侧重数量关系变化。回归分析在数据分析中占有比较重要的位置。
一元线性回归模型:指只有一个解释变量的线性回归模型,用来揭示被解释变量与另一个解释变量的线性关系。
多元线性回归模型:指含有多个揭示变量的线性回归模型,用来揭示被解释变量与多个解释变量的线性关系。
此篇文章主要讲述多元线性回归分析。
spss教程:线性回归分析——方法/步骤spss教程:线性回归分析 1、
线性回归分析的内容比较多,比如回归方程的拟合优度检验、回归方程的显著性检验、回归系数的显著性检验、残差分析、变量的筛选问题、变量的多重共线性问题。
spss教程:线性回归分析 2、
操作见图。回归分析通常需要多次试验操作才可以得出较好的模型。“方法”中选择“进入”,表示所有的自变量都进入模型,目前还没有考虑到变量的多重共线问题,要先观察初步的结果分析,才会考虑发哦变量的多重共线问题。
spss教程:线性回归分析 3、
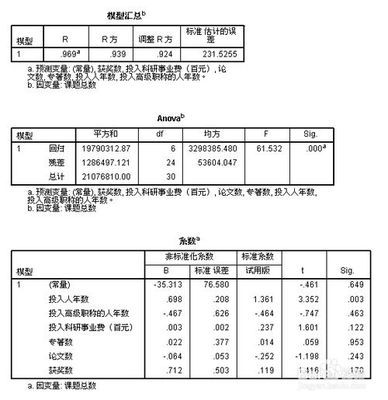
通过观察调整后的判定系数0.924,拟合优度较高,不被解释的变量较少。
由回归方程显著性检验的概率为0,小于显著性水平0.05,则认为系数不同时为0,被解释变量与解释变量全体的线性关系是显著的,可建立线性方程。
由系数表知,观察回归系数显著性检验中的概率值,如果显著性水平为0.05,除去“投入人年数”外,其他变量均大于显著性水平,这些变量保留在方程中是不正确的。所以该模型不可用,应重新建模。
spss教程:线性回归分析 4、
重新建模操作见图片,采用的是“向后筛选”方法,依次剔除的变量是专著数、投入高级职称的人年数、投入科研事业费、获奖数、论文数。最后的模型结果是“立项课题数=-94.524+0.492x投入人年数”。
spss教程:线性回归分析_回归分析
spss教程:线性回归分析 5、
残差分析:
又P-P图可知,原始数据与正态分布的不存在显著的差异,残差满足线性模型的前提要求。
由库克距离(0.041小于1)和杠杆指变量的值知,没有显著的差异。
残差点在0线周围随机分布。
spss教程:线性回归分析_回归分析
 爱华网
爱华网