在数学的学习过程中,学好基础知识是非常重要的。下面是小编为大家收集整理的初三数学基本知识点,相信这些文字对你会有所帮助的。
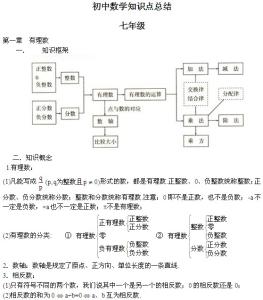
初三数学基本知识点(一)同类项的概念:所含字母相同,并且相同字母的指数也相同的项叫做同类项。几个常数项也叫同类项。
判断几个单项式或项,是否是同类项的两个标准:
①所含字母相同。②相同字母的次数也相同。
判断同类项时与系数无关,与字母排列的顺序也无关。
合并同类项的概念:把多项式中的同类项合并成一项叫做合并同类项。
合并同类项的法则:同类项的系数相加,所得结果作为系数,字母和字母的指数不变。
合并同类项步骤:
⑴.准确的找出同类项。
⑵.逆用分配律,把同类项的系数加在一起(用小括号),字母和字母的指数不变。
⑶.写出合并后的结果。
合并同类项时注意:
(1)如果两个同类项的系数互为相反数,合并同类项后,结果为0.
(2)不要漏掉不能合并的项。
(3)只要不再有同类项,就是结果(可能是单项式,也可能是多项式)。
(4)不是同类项千万不能进行合并。
初三数学基本知识点(二)因式分解定义:把一个多项式化成几个整式的积的形式的变形叫把这个多项式因式分解。
因式分解要素:①结果必须是整式 ②结果必须是积的形式 ③结果是等式
因式分解与整式乘法的关系:m(a+b+c)
公因式:一个多项式每项都含有的公共的因式,叫做这个多项式各项的公因式。
公因式确定方法:①系数是整数时取各项最大公约数。②相同字母取最低次幂③系数最大公约数与相同字母取最低次幂的积就是这个多项式各项的公因式。
提取公因式步骤:

①确定公因式。②确定商式③公因式与商式写成积的形式。
分解因式注意:
①不准丢字母
②不准丢常数项注意查项数
③双重括号化成单括号
④结果按数单字母单项式多项式顺序排列
⑤相同因式写成幂的形式
⑥首项负号放括号外
⑦括号内同类项合并。
初三数学基本知识点(三)代数定律
示物体个数的1、2、3、4...等都称为自然数。
质数与合数:一个大于1的整数,如果除了它本身和1以外不能被其它正整数所整除,那么这个数称为质数。一个大于1的数,如果除了它本身和1以外还能被其它正整数所整除,那么这个数为合数,1既不是质数又不是合数。
相反数:只有符号不同的两个实数,其中一个叫做另一个的相反数。零的相反数是零。
绝对值:一个正数的绝对值是它本身,一个负数绝对值是它的相反数,零的绝对值为零。
从数轴上看,一个实数的绝对值是表示这个数的点离开原点距离。
倒数:1除以一个非零实数的商叫这个实数的倒数。零没有倒数。
完全平方数:如果一个有理数a的平方等于有理数b,那么这个有理数b叫做完全平方数。
方根:如果一个数的n次方(n是大于1的整数)等于a,这个数叫做a的n次方根。
开方:求一数的方根的运算叫做开方。
算术根:正数a的正的n次方根叫做a的n次算术根,零的算术根是零,负数没有算术根。
代数式:用有限次运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连结所得的式子,叫做代数式。
代数式的值:用数值代替代数式里的字母,计算后所得的结果,叫做当这个字母取这个数值时的代数式的值。
代数式的分类:
有理式:只含有加、减、乘、除和乘方运算的代数式叫有理式。
无理式:根号下含有字母的代数式叫做无理式。
整式:没有除法运算或者虽有除法运算而除式中不含字母的有理式叫整式。
分式:除式中含字母的有理式叫分式。
 爱华网
爱华网