随着一部《阿凡达》票房的攀高,3D电影又被掀起了一个高潮。记得小时候在电影院里带着小眼镜看《孟良崮战役》,每到射击近镜头时就觉得枪口正对着我的眉心,那种身临其境的真实感常常让我从睡梦中惊醒。
高中开始学习绘画,造型课上老师总是在强调构图、比例、透视……老师讲的透视分为一点(平行)、两点(成角)、三点(俯视或仰视)、散点等等,当时觉得很难以接受。但无奈找不到更有效的解决二度虚拟三度空间的方法,每次画完都不免觉得画面呆板,没能将自己对对象的感受淋漓尽致地表现出来。
大学时在图书馆翻阅了大量的生物学资料,对人眼成像原理做了深入的研究学习。脱掉近视镜,裸眼,拿起望远镜,站在学校最高的建筑物上做了无数次的试验观察,终于得到了一些弧面透视方面的经验。用这种方法画场景、画静物、画风景得到了较好的效果,虽不能达到身临其境的境界,但真实可触性已经有了一些进步。
工作后有幸随恩师学习水墨山水。小时侯的枪口、战壕、丘陵再一次浮现在眼前,巍巍太行的雄浑磅礴让我一次次的早出晚归奔走其间,为的只是用笔尖触摸那份“仰望天一线,俯窥千仞壁”的气势恢弘,用心灵倾听那份“千里丰碑望不断,无情风雨任吹洒”的宽厚,然而无论怎样的意境总难以表现出太行“山峡十九转,奇峰当面立”的真实感受。
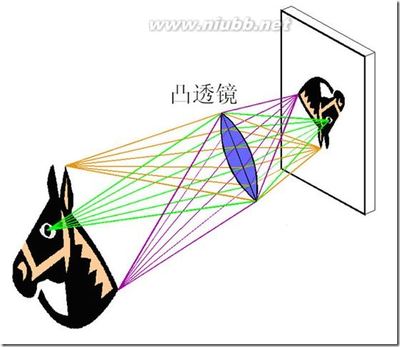
看过《阿凡达》后,我深入研究了一些双镜头模拟双眼的时差拍摄原理、双侧放映机偏振垂直播放胶片的成像原理以及部分有合成3D影像功能的软件和芯片控电眼镜等的工作原理,并且从中获得了启示。简单理解就是把两眼看到的图像分别记录,再通过左眼所见图像仅传入左眼、右眼所见图像仅传入右眼来实现人脑的3D立体合成图像功能。这与人的定点观察所得图像理论上应该一致。
不同的是电影可以利用人眼视觉暂留的1/24秒的时间差,左右放映机交替工作,使人所看到的影像还是集中在同一屏幕上,而静态的绘画作品不能利用时间差,因此在实验的初级阶段我只能借助单镜头照相机在左右眼(为了使试验效果更加明显,我选择了比左眼更左一点、比右眼更右一点的视点)处分别对同一组对象进行拍照记录,然后打印成等幅照片,分别在左眼和右眼的最佳视距处垂直于视线放置。观察过程中始终用一不透明隔板放在双眼连线的中垂线上,以分隔双眼的视域范围。这有点像马的眼睛会出现盲区,但并不影响实验结果。结果表明这样做大脑合成的图像立体感甚至要超出人的正常观察结果,我想大概是因为人眼观察对象时双侧眼球的游移导致的。
有了这样的实验结果,我更加肯定了双眼透视理论研究的可行性。接下来的难题就是如何把左右视点的成像拼合在一起。简单的电脑对叠处理后,就会出现像脱掉专用眼镜直接看幕布3D电影一样的模糊重影的图像。我们要的当然不是必须戴上专用眼镜才能欣赏的平面艺术,于是我带着如何合成左右视点图片的困惑又做了很多试验。
一系列试验的无果而终,使我最后又不得不回到平面透视的起点上来。初学透视时,由于找不准焦点,老师经常督促我闭上一只眼睛用铅笔量静物结构线的方向,而每次闭上的眼睛都必须相同。这实际上就是跟单镜头摄像机的镜头一样,是单焦点透视。而我最初想要的只是真实感而已,跟焦点在哪、视心点在哪并无大的关联。又想起正方体平行透视讲解示意图中标示的视心点(焦点)多在静物外侧。而视心点的定义为:视点到视平线的垂心,即从视点(人眼睛)向视平线做垂线得到的垂足。视线的定义为:以人眼为顶点的射线——视点与物体任何部位的假想连线,非阻挡则延伸。视平线的定义为:与人眼等高的一条水平线。我们不妨坐下来演示一下:观者保持静止状态则视点不变;在观者的左前方、正前方、右前方分别放置三个物体,在观察三个物体时会产生三个方向的视线、视平线。线性透视理论中对视平线的罗盘方向并没有严格的规定,仅对高度和水平做了明确规定。也就是说总有一个方向的水平线会与视线相垂直,那么视心点也一定将会出现在物体左右剪影切线的延长线之间,也就等于是在同一视点分别直视三个物体,而得到的是各自独立的三张透视成像图。根据这一结果,我在对太行山写生中尝试运用了这种视点不变移动焦点的透视方法,打破了原来的以组排列单一视点的构图方式,取得了较为真实的画面二维假设三维空间的效果。在具体测绘焦点的过程中,我没有始终闭起一只眼睛,而是采取交替用左右眼测试最后取中点的方式。这种方法可以使视距延长,就像炮兵用大拇指测视距一样,会得到较为准确的距离。
当然,这种用双眼交替测视距,在双眼叠加视域范围内视点不变移动视心点(焦点参照),把每个物体或每段距离都当作独立的再现对象独立进行线透视的方法仍然没有进行到最后阶段,我将继续用试验论证此法的可行性。在此暂且称其为模拟3D成像原理的透视理论研究,愿与同样追求平面再现三维真实性的朋友共同探讨。
 爱华网
爱华网