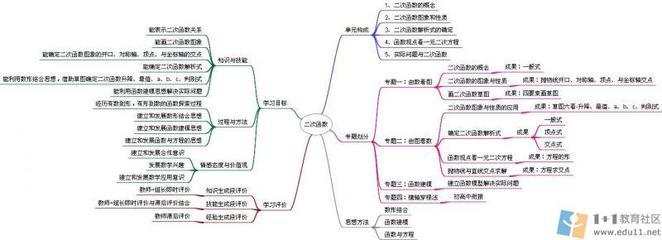
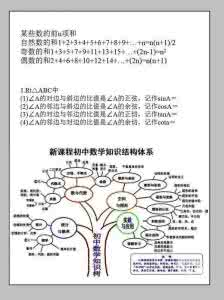
二次函数(quadratic function)的基本表示形式为y=ax²+bx+c(a≠0)。二次函数最高次必须为二次, 二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。今天小编要与大家分享的是:二次函数在高中阶段的应用相关数学论文。具体内容如下,欢迎阅读:
二次函数在高中阶段的应用在初中教材中,对二次函数作了较详细的研究,由于初中学生基础薄弱,又受其接受能力的限制,这部份内容的学习多是机械的,很难从本质上加以理解。进入高中以后,尤其是高三复习阶段,要对他们的基本概念和基本性质(图像以及单调性、奇偶性、有界性)灵活应用,对二次函数还需再深入学习。
一、进一步深入理解函数概念初中阶段已经讲述了函数的定义,进入高中后在学习集合的基础上又学习了映射,接着重新学习函数概念,主要是用映射观点来阐明函数,这时就可以用学生已经有一定了解的函数,特别是二次函数为例来加以更深认识函数的概念。二次函数是从一个集合A(定义域)到集合B(值域)上的映射ƒ:A→B,使得集合B中的元素y=ax2+bx+c(a≠0)与集合A的元素X对应,记为ƒ(x)= ax2+ bx+c(a≠0)这里ax2+bx+c表示对应法则,又表示定义域中的元素X在值域中的象,从而使学生对函数的概念有一个较明确的认识,在学生掌握函数值的记号后,可以让学生进一步处理如下问题:
类型I:已知ƒ(x)= 2x2+x+2,求ƒ(x+1)
这里不能把ƒ(x+1)理解为x=x+1时的函数值,只能理解为自变量为x+1的函数值。
类型Ⅱ:设ƒ(x+1)=x2-4x+1,求ƒ(x)
这个问题理解为,已知对应法则ƒ下,定义域中的元素x+1的象是x2-4x+1,求定义域中元素X的象,其本质是求对应法则。
一般有两种方法:
(1)把所给表达式表示成x+1的多项式。
ƒ(x+1)=x2-4x+1=(x+1)2-6(x+1)+6,再用x代x+1得ƒ(x)=x2-6x+6
(2) 变量代换:它的适应性强,对一般函数都可适用。
令t=x+1,则x=t-1 ∴(t)=(t-1)2-4(t-1)+1=t2-6t+6从而ƒ(x)= x2-6x+6
二、二次函数的单调性,最值与图像。在高中阶阶段学习单调性时,必须让学生对二次函数y=ax2+bx+c在区间(-∞,-b2a]及[-b2a,+∞) 上的单调性的结论用定义进行严格的论证,使它建立在严密理论的基础上,与此同时,进一步充分利用函数图像的直观性,给学生配以适当的练习,使学生逐步自觉地利用图像学习二次函数有关的一些函数单调性。
类型Ⅲ:画出下列函数的图像,并通过图像研究其单调性。
(1)y=x2+2|x-1|-1
(2)y=|x2-1|
(3)= x2+2|x|-1
这里要使学生注意这些函数与二次函数的差异和联系。掌握把含有绝对值记号的函数用分段函数去表示,然后画出其图像。
类型Ⅳ设ƒ(x)=x2-2x-1在区间[t,t+1]上的最小值是g(t)。
求:g(t)并画出 y=g(t)的图像
解:ƒ(x)=x2-2x-1=(x-1)2-2,在x=1时取最小值-2
当1∈[t,t+1]即0≤t≤1,g(t)=-2
当t>1时,g(t)=ƒ(t)=t2-2t-1
当t<0时,g(t)=ƒ(t+1)=t2-2
t2-2, (t<0)
g(t)= -2,(0≤t≤1)
t2-2t-1, (t>1)
首先要使学生弄清楚题意,一般地,一个二次函数在实数集合R上或是只有最小值或是只有最大值,但当定义域发生变化时,取最大或最小值的情况也随之变化,为了巩固和熟悉这方面知识,可以再给学生补充一些练习。
如:y=3x2-5x+6(-3≤x≤-1),求该函数的值域。
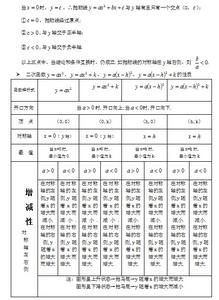
三、二次函数的知识,可以准确反映学生的数学思维:
类型Ⅴ:设二次函数ƒ(x)=ax2+bx+c(a>0)方程ƒ(x)-x=0的两个根x1,x2满足0
 爱华网
爱华网