最近,债券市场出现了一些波动,投资者对于债券市场也有了更多的关注,在很多关于债券的分析文章或者投资建议中,常常出现“久期”这个词。那么久期是什么意思呢?下面就让爱华网小编带着大家一起去了解一下什么是债券久期的规则吧。
债券久期的数学解释
久期(Duration)
『久期,全称麦考雷久期-Macaulayduration,数学定义
如果市场利率是Y,现金流(X1,X2,...,Xn)的麦考雷久期定义为:D(Y)=[1*X1/(1+Y)^1+2*X2/(1+Y)^2+...+n*Xn/(1+Y)^n]/[X0+x1/(1+Y)^1+X2/(1+Y)^2+...+Xn/(1+Y)^n]
即D=(1*PVx1+...n*PVxn)/PVx
其中,PVXi表示第i期现金流的现值,D表示久期。
通过下面例子可以更好理解久期的定义。
例子:假设有一债券,在未来n年的现金流为(X1,X2,...Xn),其中Xi表示第i期的现金流。假设利率为Y0,投资者持有现金流不久,利率立即发生变化,变为Y,问:应该持有多长时间,才能使得其到期的价值不低于的价值?
通过下面定理可以快速解答上面问题。
定理:PV(Y0)*(1+Y0)^q<=PV(Y)(1+Y)^q的必要条件是q=D(Y0)。这里D(Y0)=(X1/(1+Y0)+2*X2/(1+Y0)^2+...+n*Xn/(1+Y0)^n)/PV(Y0)
q即为所求时间,即为久期。
上述定理的证明可通过对Y导数求倒数,使其在Y=Y0取局部最小值得到。(容易)
浅显易懂的解释:久期就是债券价格相对于利率水平正常变动的敏感度。如果一只短期债券基金的投资组合久期是2.0,那么利率每变化1个百分点,该基金价格将上升或下降2%;一只长期债券型基金的投资组合久期是12.0,那么利率每变化1个百分点,其价格将上升或下降12%。
债券久期的发展
修正久期
从上面的讨论中可知:对于给定的到期收益率的微小变动,债券价格的相对变动与其Macaulay久期成比例。当然,这种比例关系只是一种近似的比例关系,它的成立是以债券的到期收益率很小为前提的。为了更精确地描述债券价格对于到期收益率变动的灵敏性,又引入了修正久期模型(ModifiedDurationModel)。修正久期被定义为:△P/P=-(D*)dy+C[(dy)^2]/2
从这个式子可以看出,对于给定的到期收益率的微小变动,债券价格的相对变动与修正久期之间存在着严格的比例关系。所以说修正久期是在考虑了收益率项y的基础上对Macaulay久期进行的修正,是债券价格对于利率变动灵敏性的更加精确的度量。
有效久期
在Macaulay久期模型研究中存在一个重要假设,即随着利率的波动,债券的现金流不会发生变化。然而这一假设对于具有隐含期权的金融工具,如按揭贷款、可赎回(或可卖出)债券等而言则很难成立。因此,Macaulay久期模型不应被用来衡量现金流易受到利率变动影响的金融工具的利率风险。针对Macaulay久期模型这一局限,FrankFabozzi提出了有效久期的思想。所谓有效久期是指在利率水平发生特定变化的情况下债券价格变动的百分比。它直接运用不同收益率变动为基础的债券价格进行计算,这些价格反映了隐含期权价值的变动。其计算公式为:
Duration(effective)=(V-Δy-V+Δy)÷2V0Δy[2]
其中:
V-Δy利率下降x个基点时债券价格;
V+Δy利率上升x个基点时债券价格;
-Δy初始收益率加上x个基点;
+Δy初始收益率减去x个基点;
V0债券初始价格;
有效久期不需要考虑各期现金流的变化情况,不包含利率变化导致现金流发生变化的具体时间,而只考虑利率一定变化下的价格总体情况。因此,有效久期能够较准确地衡量具有隐含期权性质的金融工具的利率风险。对于没有隐含期权的金融工具,有效久期与Macaulay久期是相等的。
随着对久期模型研究的不断深入,相继有人提出了方向久期、偏久期、关键利率久期、近似久期以及风险调整久期等新的久期模型,把利率的期限结构、票息率的改变以及信用风险、赎回条款等加入到模型里面,使久期模型得到了进一步的发展。
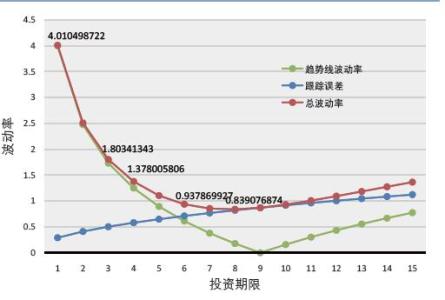
债券组合久期
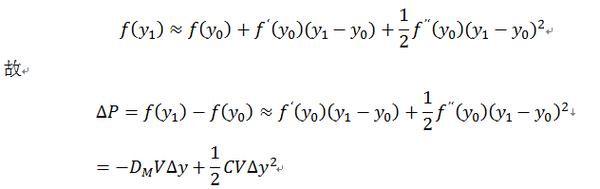
债券投资组合也有相应的久期概念,其久期为单个久期的加权平均,可以用下面的公式进行计算:
其中为单个债券在组合中的权重。
债券久期的用途
在债券分析中,久期已经超越了时间的概念,利率上升所引起的债券价格下降幅度就越大,而利率下降所引起的债券价格上升幅度也越大。可见,同等要素条件下,修正久期小的债券比修正久期大的债券抗利率上升风险能力强,但抗利率下降风险能力较弱。
正是久期的上述特征给我们的债券投资提供了参照。当我们判断当前的利率水平存在上升可能,就可以集中投资于短期品种、缩短债券久期;而当我们判断当前的利率水平有可能下降,则拉长债券久期、加大长期债券的投资,这就可以帮助我们在债市的上涨中获得更高的溢价。
需要说明的是,久期的概念不仅广泛应用在个券上,而且广泛应用在债券的投资组合中。一个长久期的债券和一个短久期的债券可以组合一个中等久期的债券投资组合,而增加某一类债券的投资比例又可以使该组合的久期向该类债券的久期倾斜。所以,当投资者在进行大资金运作时,准确判断好未来的利率走势后,然后就是确定债券投资组合的久期,在该久期确定的情况下,灵活调整各类债券的权重,基本上就能达到预期的效果。
久期是一种测度债券发生现金流的平均期限的方法。由于债券价格敏感性会随着到期时间的增长而增加,久期也可用来测度债券对利率变化的敏感性,根据债券的每次息票利息或本金支付时间的加权平均来计算久期。
久期的计算就当是在算加权平均数。其中变量是时间,权数是每一期的现金流量,价格就相当于是权数的总和(因为价格是用现金流贴现算出来的)。这样一来,久期的计算公式就是一个加权平均数的公式了,因此,它可以被看成是收回成本的平均时间。
决定久期即影响债券价格对市场利率变化的敏感性包括三要素:到期时间、息票利率和到期收益率。
不同债券价格对市场利率变动的敏感性不一样。债券久期是衡量这种敏感性最重要和最主要的标准。久期等于利率变动一个单位所引起的价格变动。如市场利率变动1%,债券的价格变动3%,则久期是3。
 爱华网
爱华网